方差分析

什么是方差分析

用数理统计分析试验结果、鉴别各因素对结果影响程度的方法称为方差分析（Analysis Of Variance），记作 ANOVA。

单因素方差分析(One Way Analysis of Variance)

是什么？

A 取某个水平下的指标视为随机变量，判断 A 取不同水平时指标有无显著差别，相当于检验若干总体的均值是否相等。（A为影响因子）

数学模型

section1

A取r个水平$A_1,A_2,...A_r$,在各个水平下的影响指标服从$N(\mu_i,\sigma ^2)(i=1\ldots r)$
每个水平下抽取$n_i$个样本。

假设检验：

$H_0: \mu_1=\mu_2=\cdots=\mu_r ; H_1: \mu_1, \mu_2, \cdots, \mu_r$ 不全相等
由于$x_{ij}$同时受到$A_i$和随机因素的影响：
$$
x_{ij}=\mu_i+\epsilon_{ij}
$$
其中$\epsilon$~$N(0,\sigma^2)$
记$\mu，n$分别为整体数据集均值和数据集大小。

统计分析

记：
$$
S_T = \sum_{i=1}^r\sum_{j=1}^{n_r}(x_{ij}-\bar x)^2
\\
S_E = \sum_{i=1}^r\sum_{j=1}^{n_r}(x_{ij}-\bar x_{i.})^2
\\
S_A(S_B) = \sum _{i=1}^r n_i(\bar x_{i.}-\bar x)^2
$$
回顾:

$\chi^2$分布：[百度百科](卡方分布_百度百科 (baidu.com))
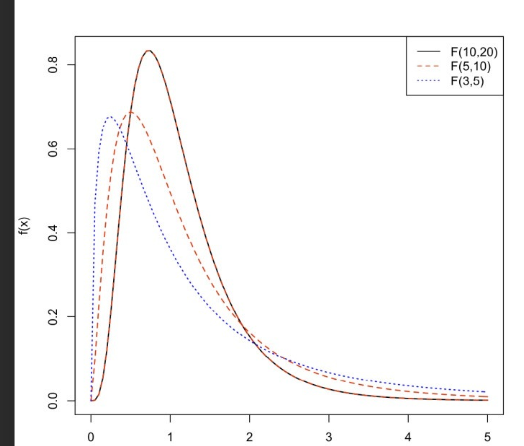
$F$分布：[百度百科](F分布_百度百科 (baidu.com))
自由度DF(degree of dreedom)：[百度百科]()(F分布_百度百科 (baidu.com))

有：

$\frac{S_E}{\sigma^2}$~$\chi^2(\sum_{i=1}^r(n_i-1))$即为$\chi^2(n-r)$
$\frac{S_A(S_B)}{\sigma^2}$~$\chi^2(r-1)$
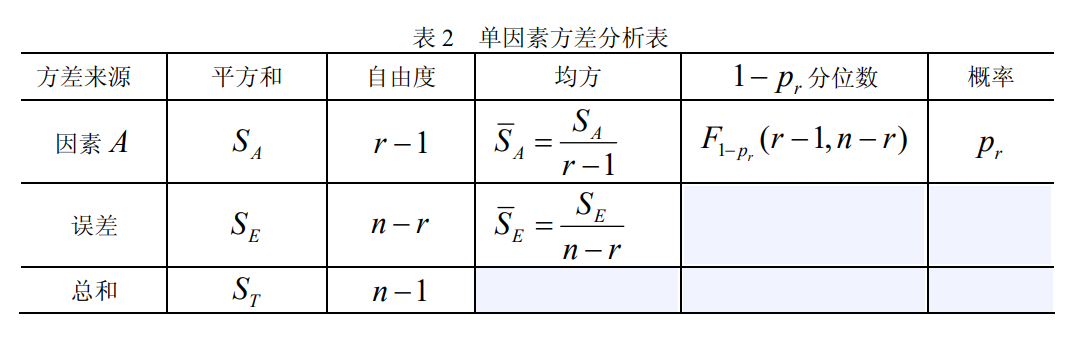
其中$F = \frac{\bar S_A}{\bar S_{E}}$

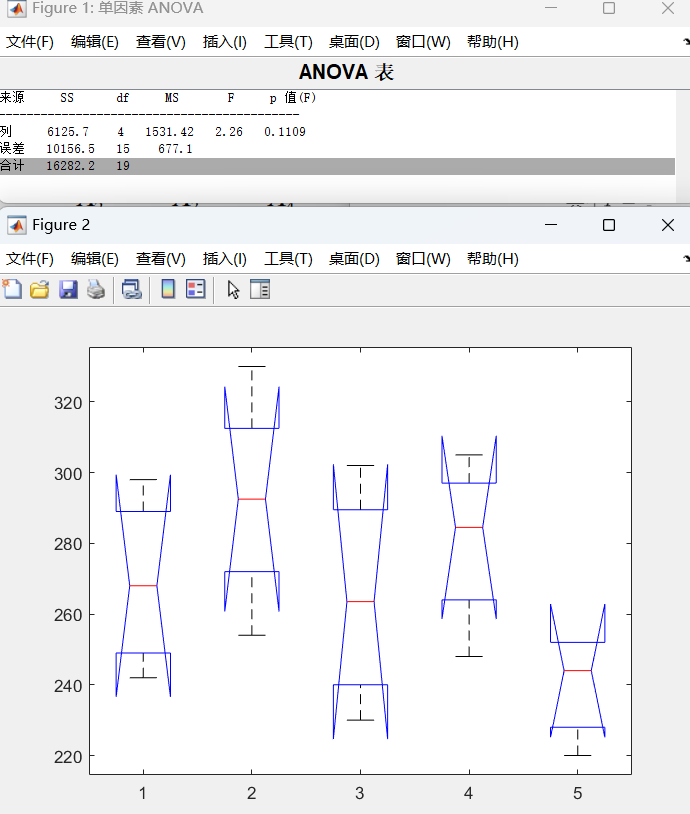
具体实现实验，使用MATLBA、SPSS或者EXCEL均可。

x=[256 254 250 248 236 
 242 330 277 280 252 
 280 290 230 305 220 
 298 295 302 289 252];
 p=anova1(x)

方差分析一般用的显著性水平是: 取 $\alpha=0.01$, 拒绝 $H_0$, 称因素 $A$ 的影响（或 $A$ 各水平的差异) 非常显著; 取 $\alpha=0.01$, 不拒绝 $H_0$, 但取 $\alpha=0.05$, 拒绝 $H_0$, 称因素 $A$ 的影响显著; 取 $\alpha=0.05$, 不拒绝 $H_0$ ，称因素 $A$ 无显著影响。

方差分析