随机过程
Chapter 1
主要是有关概率论的一些复习知识,由于概率论已经学习完毕,我只整理一些新的知识点:
-
这是离散概率计算的又一种方法:
-

-
矩母函数

好的性质:
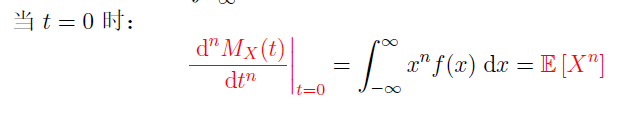
马氏链(Markov chain)
定义
-
定义:如果 $p_{n+1}(i, j)=\mathbb{P}\left(X_{n+1}=j \mid X_n=i\right)$, 称这个过程具有马氏性 (Markov property)。即: $X_{n+1}$ 只与 $X_n$ 有关, 而与之前的状态 $\left(X_{n-1}, \ldots, X_0\right)$ 无关。
-
如果时刻 $n$ 的取值与转移概率无关, 即
$$
\mathbb{P}\left(X_{n+1}=j \mid X_n=i\right)=p(i, j), \mid \quad \forall n
$$
则称为时齐性 (time-homogeneous), 相应的马氏链称作时齐马氏链。
状态转移
$p(i, j)=\mathbb{P}\left(X_{n+1}=j \mid X_n=i\right)$ 给出了从状态 $i$ 到 $j$ 的一步转移概率; 类似地, 从 $i$ 到 $j$ 的 $m$ 步 $(m>1)$ 转移概率定义为:
$$
p^m(i, j)=\mathbb{P}\left(X_{n+m}=j \mid X_n=i\right)
$$
这里的 $p^m(i, j)$ 是 $m$ 步转移矩阵 $\mathbf{P}^m$ 第 $i$ 行、第 $j$ 列的数值。
定义 $m$ 步转移矩阵是 1 步转移矩阵 $\mathbf{P}$ 的 $m$ 次幕, 即 $\mathbf{P}^m$
Chapman-Kolmogorov 方程
$$
p^{m+n}(i, j)=\mathbb{P}\left(X_{m+n}=j \mid X_0=i\right)=\sum_k p^m(i, k) \cdot p^n(k, j)
$$
推论:
$$
p^{m+n}(i, j) \geq p^m(i, k) \cdot p^n(k, j), \quad \forall k
$$
状态的分类
几个重要的标记:
- $\mathbb{P}_x(A)=\mathbb{P}\left(A \mid X_0=x\right)$, 初始时刻状态为 $x$ 的条件下, 事件 $\mathrm{A}$ 发生的概率
- $T_y=\min \left\{n: n \geq 1, X_n=y\right\}$, 首次返回状态 $y$ 的最短时间
$T_y$ 可看作一个停时 (stopping time) - $\rho_{y y}=\mathbb{P}_y\left(T_y<\infty\right)$, 从初始时刻状态 $y$, 经过有限步首次返回到状态 $y$ 的概率



可达与互通



弄清楚常返态的例题

